จากบทนิยามของฟังก์ชันเอกซ์โพเนนเชียล ฟังก์ชันนี้มีรูปแบบในรูปของเลขยกกำลัง
โดยฐานของมันต้องมากกว่า 0 และฐานต้องไม่เป็น 1 อ่านต่อ
วันเสาร์ที่ 24 มกราคม พ.ศ. 2558
ฟังก์ชันขั้นบันได
ฟังก์ชันขั้นบันได หมายถึง
ฟังก์ชันที่มีโดเมนเป็นสับเซตของจำนวนจริง และมีค่าของฟังก์ชันเป็นค่าคงตัวเป็นช่วงๆ
มากกว่าสองช่วง กราฟของฟังก์ชันนี้มีลักษณะคล้ายขั้นบัน อ่านต่อ
ฟังก์ชันกำลังสอง
ฟังก์ชันกำลังสอง
คือ ฟังก์ชันที่อยู่ในรูป y
= ax2 +
bx + c เมื่อ a, b, c เป็นจำนวนจริงใดๆ และ a ≠ 0
ลักษณะของกราฟของฟังก์ชันขึ้นอยู่กับค่าของ a, b และ c เมื่อ a เป็นจำนวนบวกหรือจำนวนลบ
จะทำให้ได้กราฟเป็นเส้นโค้งหงายหรือคว่ำ อ่านต่อ
ความสัมพันธ์ของฟังก์ชัน
ในชีวิตประจำวันเรามักพบ
สิ่งที่มีความเกี่ยวข้องกันอยู่เสมอ เช่น สินค้ากับราคาของสินค้า
คนไทยทุกคนจะต้องมีเลขประจำตัวประชาชนเป็นของตนเอง
ตัวอย่างที่กล่าวมาเป็นตัวอย่างที่แสดงความสัมพันธ์ของสิ่งสองสิ่งที่เกี่ยว
ข้องกันภายใต้กฎเกณฑ์อย่างใดอย่างหนึ่ง
สำหรับในวิชาคณิตศาสตร์มีสิ่งที่แสดงความสัมพันธ์ดังตัวอย่างต่อไปนี้ อ่านต่อ
สมการกำลังสอง
สมการกำลังสองที่มีรูปทั่วไปเป็น
ax2 + bx + c = 0 เมื่อ a , b , c เป็นค่าคงตัว และ a ไม่เท่ากับ 0
ทำได้โดยอาศัยการแยกตัวประกอบ หาจำนวนเต็มสองจำนวนที่คูณกันได้ c และบวกกันได้ b อ่านต่อ

สมบัติของจำนวนจริง
สมบัติของจำนวนจริงเกี่ยวกับการบวกและการคูณ
มีดังนี้
1. สมบัติปิด
2.
สมบัติการสลับที่
3.
สมบัติการเปลี่ยนกลุ่ม
4.
สมบัติการมีเอกลักษณ์
5.
สมบัติการมีอินเวอร์ส
6.
สมบัติการแจกแจง
จำนวนจริง
มนุษย์รู้จักการใช้จำนวน
มาตั้งแต่สมัยดึกดำบรรพ์โดยใช้ก้อนหินหรือใช้รอยบากบนต้นไม้แสดงจำนวนสัตว์ เลี้ยง
กล่าวได้ว่าจำนวนชนิดแรกที่มนุษย์รู้จักคือจำนวนนับ ต่อมา
ภายหลังเมื่อโลกมีการพัฒนามากขึ้น มนุษย์จึงพัฒนาจำนวนชนิดอื่นๆ
ขึ้นมาเพื่อให้สามารถแทนปริมาณต่างๆ เช่น น้ำหนัก อุณหภูมิ จำนวนประชากร
ความยาวของเส้นรอบวงของโลก ฯลฯ จำนวนซึ่งสามารถแทนสิ่งเหล่านี้ได้ เรียกว่า
จำนวนจริง เซตของจำนวนจริงประกอบด้วย

การให้เหตุผลแบบนิรนัย
การให้เหตุผลแบบนิรนัยเป็นการนำความรู้พื้นฐานซึ่งอาจเป็นความเชื่อ
ข้อตกลง กฎ หรือบทนิยาม ซึ่งเป็นสิ่งที่รู้มาก่อน
และยอมรับว่าเป็นความจริงเพื่อหาเหตุผลนำไปสู่ข้อสรุป
เป็นการอ้างเหตุผลที่มีข้อสรุปตามเนื้อหาสาระที่อยู่ภายในขอบเขตของข้ออ้างที่กำหนด
ตัวอย่างที่ 1 เหตุ
1.สัตว์เลี้ยงทุกตัวเป็นสัตว์ไม่ดุร้าย
2. แมวทุกตัวเป็นสัตว์เลี้ยง
ผล แมวทุกตัวเป็นสัตว์ไม่ดุร้าย

การให้เหตุผลแบบอุปนัย
การให้เหตุผลแบบอุปนัย
(Inductive Reasoning)
การให้เหตุผลแบบอุปนัย
เป็นวิธีการสรุปผลมาจากการค้นหาความจริงจากการสังเกตหรือการทดลองหลายครั้งจากกรณีย่อยๆ
แล้วนำมาสรุปเป็นความรู้แบบทั่วไป
การหาข้อสรุปหรือความจริงโดยใช้วิธีการให้เหตุผลแบบอุปนัยนั้น ไม่จำเป็นต้องถูกต้องทุกครั้ง เนื่องจากการให้เหตุผลแบบอุปนัยเป็นการสรุปผลเกิดจากหลักฐานข้อเท็จจริงที่มีอยู่
ดังนั้นข้อสรุปจะเชื่อถือได้มากน้อยเพียงใดนั้นขึ้นอยู่กับลักษณะของข้อมูล หลักฐานและข้อเท็จจริงที่นำมาอ้างซึ่งได้แก่
1. จำนวนข้อมูล
หลักฐานหรือข้อเท็จจริงที่นำมาเป็นข้อสังเกตหรือข้ออ้างมีมากพอกับการสรุปความหรือไม่
เช่น
ถ้าไปทานส้มตำที่ร้านอาหารแห่งหนึ่งแล้วท้องเสีย แล้วสรุปว่า
ส้มตำนั้นทำให้ท้องเสีย การสรุปเหตุการณ์นั้นอาจเกิดขึ้นเพียงครั้งเดียว
ย่อมเชื่อถือได้น้อยกว่าการที่ไปรับประทานส้มตำบ่อยๆแล้วท้องเสียเกือบทุกครั้ง
2. ข้อมูล หลักฐานหรือข้อเท็จจริง
เป็นตัวแทนที่ดีในการให้ข้อสรุปหรือไม่ เช่น
ถ้าอยากรู้ว่าคนไทยชอบกินข้าวเจ้าหรือข้าวเหนียวมากกว่ากัน
ถ้าถามจากคนที่อาศัยอยู่ในภาคเหนือหรือภาค-อีสาน
คำตอบที่ตอบว่าชอบกินข้าวเหนียวอาจจะมีมากกว่าชอบกินข้าวจ้าว แต่ถ้าถามคนที่อาศัยอยู่ในภาคกลางหรือภาคใต้
คำตอบอาจจะเป็นในลักษณะตรงกันข้าม อ่านต่อ

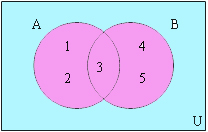
เอกภพสัมพัทธ์
เอกภพสัมพัทธ์ คือ
เซตที่ประกอบด้วยสมาชิกทั้งหมดของสิ่งที่เราต้องการจะศึกษา
สามารถเขียนแทนได้ด้วยสัญลักษณ์ u
เอกภพสัมพัทธ์ (Relative Universe) ในการพูดถึงเรื่องใดก็ตามในแง่ของเซต
เรามักมีขอบข่ายในการพิจารณาสมาชิกของเซตที่จะกล่าวถึง โดยมีข้อตกลงว่าเราจะไม่กล่าวถึงสิ่งใดนอกเหนือไปจากสมาชิก
ของเซตที่กำหนดขึ้น เช่น
ถ้าเรากำหนดเซตของสมาชิกทุกคนในครอบครัวของผู้เรียนเองให้เป็นเซตใหญ่ที่สุด เราจะเรียกเซตนี้ว่า เอกภพสัมพัทธ์ เขียนแทนด้วยสัญลักษณ์ U โดยมีข้อตกลงว่า เมื่อกล่าวถึงสมาชิกของเซตใด ๆ จะไม่กล่าวถึงสิ่งอื่นที่นอกเหนือจากสมาชิกในเอกภพสัมพัทธ์
กำหนดให้ U คือ เซตของจำนวนจริง
และ

เซต
เซต
ใช้แทนกลุ่มของคน,สัตว์,สิ่งของ หรือสิ่งที่เราสนใจ
เราใช้เครื่องหมายปีกกา“{
} ”
แสดงความเป็นเซต
และสิ่งที่อยู่ภายในปีกกา
เราเรียกสมาชิกของเซต
เซตที่เท่ากัน
เซต 2
เซตจะเท่ากันก็ต่อเมื่อจำนวนสมาชิกและสมาชิกของทั้ง 2 เซต เหมือนกันทุกตัว
เช่น A={1,2,3}
B={1,2,3} จะได้ A=B
เซตที่เทียบเท่ากัน
เซต 2 เซตจะเทียบเท่ากันก็ต่อเมื่อ
จำนวนสมาชิกของทั้ง 2 เซต เท่ากัน
เช่น
A={a,b,c} ,
B={1,2,3}
สมัครสมาชิก:
ความคิดเห็น (Atom)